注 6. 定理 5 の証明では、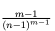
は m が大きくなるにつれゼロに近づくという事実を使用しています。有名なことですが、高校生の中にはこれを知らない人もいるかもしれません。
定理 7. n ≥ 3 の各整数について、正 n 角形は指定された円に内接するすべての n 辺の多角形中で最大の面積を持ちます。
証明。 a1、a2,...,an を多角形の中心角とします。定理 5 により、(c)iの演算を適用すると、多角形の面積は正多角形の面積に近づいて大きくなります。定理 2 の過程で面積は常に増加すると我々は説明しました。こうして、正多角形は、円に内接する多角形の中で最も面積が大きい。
4.容器の水位が異なる問題
定理 5 は以下の問題に適用できます。図 3 に水の容器のグループがあり、隣接する 2 つの容器の水位を同じにする操作があります。 この操作の例を図 3、4、および 5 に示します。図 4 では、6 番目の容器と 7 番目の容器の間のスリットを削除します。すると、2 つの容器の水位は同じになります。続いてスリットを図 5 に示すように、戻していきます。ご覧のとおり、この操作は定理 5 で使用したものと数学的には同じです。定理 5 により、操作を繰り返し適用することで、容器のレベルを図 3 のレベルの平均に近づけることができます。
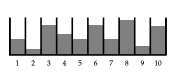
図３：水位 １
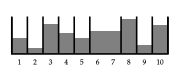
図４：水位 ２
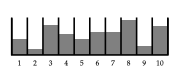
図５：水位 ３
5.付録
ここでは、[2] で示されている、円に内接する n 角形の間で正 n 角形が最大であるという証明の概要を説明します。証明は短くて良いですが、この記事の上記の証明とは異なり、上級レベルの微積分に依存します。
証明。 D を Rn 内のベクトルのセットとし、自己交差しない環状多角形の辺によって定められる角度を表すもの (長さ 0 の辺を持つことが許可されます)とします。この場合、D は明らかに閉じた有界集合であり、したがってコンパクトです。f(v) をベクトル v ∈ D で記述される多角形 P の面積とします。このとき、f(v) は D 内で連続です。上級レベルの微積分の定理では、各連続関数がコンパクトなセット上で最大値に達すると述べています。したがって、f(v) は D で最大値に達します。f(a) が a ∈ D の最大値とし、R を a によって記述される多角形とします。R が正則でない場合、R には長さが等しくない 2 つの辺 AB と BC があります。B を円弧上で動かして AB と BC の長さを等しくします。これにより、新しい多角形の面積が R より大きく、矛盾しています。したがって、R は正則 (正多角形) です。