この手順を m 回繰り返すと、角度の合計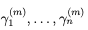 
は
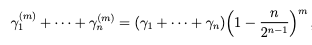
を満たし、m → ∞ になるほど和は 0 に収束します。したがって、角度間の差は、2 つの演算を繰り返し中心角に適用すると、0 になる傾向があります。
(a) と (b) の演算を繰り返し適用することで、各中心角度は 
に収束します。したがって、多角形の面積は、正多角形に近づくほど増加します。
これは、円に内接する 2n 辺の多角形の面積が同じ円に内接する正２ｎ角形のそれ以下であることを示します。したがって、正多角形は、円に内接する多角形の中で最も面積が大きいです。
注意 3 定理 2 の証明では、証明を数学的に厳密にするために二項定理と数学的帰納法を使用する必要があります。ただし、これらがなくても理解できます。
３．任意の数の辺を持つ多角形
このセクションでは、n ≥ 3 の任意の自然数である n 辺多角形の (*) を証明します。ここでは、前のセクションよりも多くの数学の知識を使用します。数列の極限に関連する数学的帰納法と計算が必要です。証明に使用される計算は非常に複雑に見えるかもしれません。しかし、直感的説明すると、高校生であればこれらの考えを理解できると考えています。
定義 4.任意の実数の数列に対する以下の演算を定義します。b1、b2 ..., bn および 1 ≤ i < n の任意の整数 i:
(c)iこの操作により数列が作成されます
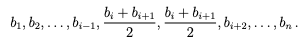
定理 5. a1、a2,...,an を実数の数列とし、s = a1 + a2 + · · · + an とします。
(c)i の演算を繰り返し適用することで、すべての i = 1, 2,..., n で、数列を取得します。
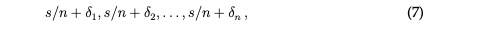
実数の場合 δ1、δ2,...,δn、ここで |δ1|、|δ2|,...,|δn| は必要に応じて小さくすることができます。言い換えると、結果の数列内の各数値は s/n に収束します。
証明。 この定理を数学的帰納法によって証明します。n = 2 の場合、演算 (c)1 を a1、a2 に適用すると、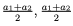
が得られます。したがって、(7) は n = 2 に対して有効です。この場合、δ1 = δ2 = 0 です。
この定理は n − 1 に対して有効であると仮定し、n の場合を証明します。ここで n ≥ 3です。a1、a2,...an から始め、(c)i を十分な回数 a1、a2,...,an−1 に適用して数列 dk + δ1, dk + δ2,...,dk + δn−1 を取得しますが、実数の場合 dk, δ1, δ2,..., δn−1 であり,ここで |δ1|、|δ2|,...,|δn−1| は必要に応じていくらでも小さくすることができます。残り (最後) の数は s − (n − 1)dk − (δ1 + · · · + δn−1) です。 したがって、以下の数列が得られます。