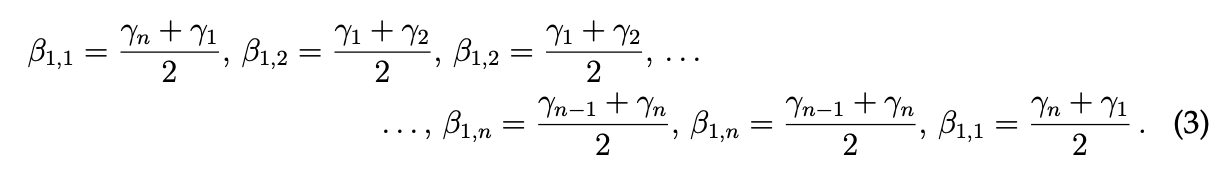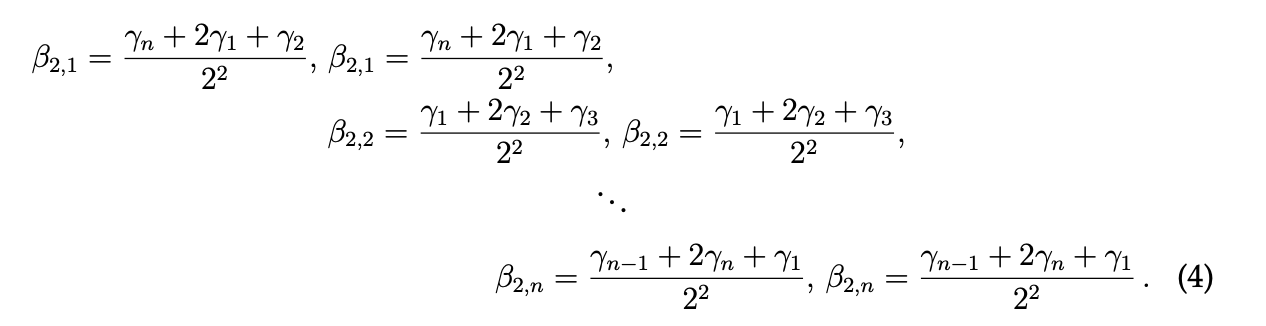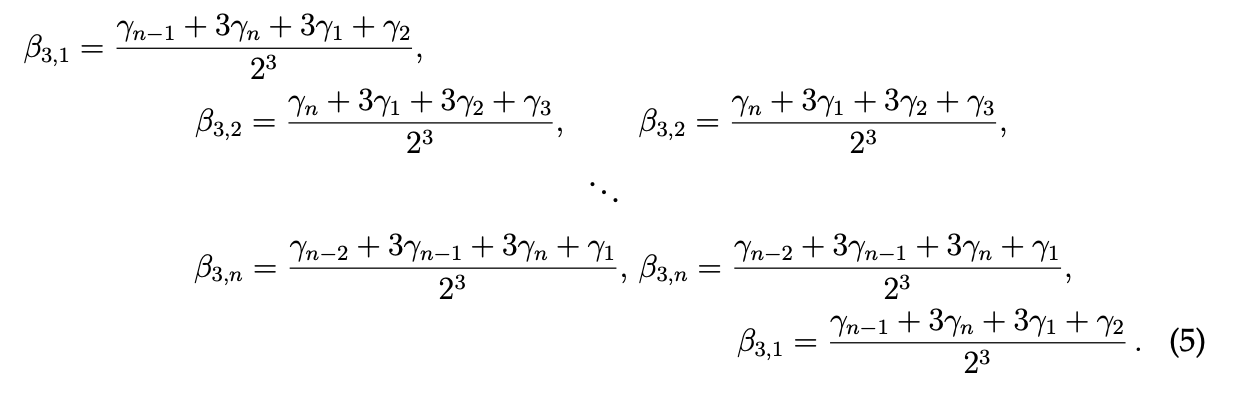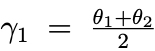なので、|P1P3| = |Q1Q3| になります。したがって、三角形 △Q1Q2Q3 の底辺は、△P1P2P3 と同じです。|Q1Q2| = |Q2Q3| 故に △Q1Q2Q3 の高さは △P1P2P3 より大きいです。すると、△Q1Q2Q3 の面積は △P1P2P3 の面積より大きく、多角形 Q1Q2Q3O の面積は多角形 P1P2P3O の面積より大きいです。同様に、多角形 QiQi+1Qi+2O は、i = 2, 3, ...,2n-3 の場合 PiPi+1Pi+2O よりも大きくなります。私たちはまた多角形
Q2n-1Q2nQ1O が多角形 P2n-1P2nP1O よりも大きいことも証明できます。
これらの多角形の面積を加算することにより、以下のことが証明されます: 多角形の面積 Q1Q2・・・QnQ1 は多角形 P1P2・・・PnP1 より大きいです。
故に、演算(ａ) を θ１、θ２,...,θ2n に適用すると、
が得られ、演算 (a) を多角形の辺の中心角に適用すると、より大きな多角形が得られます。多角形の辺の中心角に演算 (b) を適用すると同じことが言えます。
次に、(2) に操作 (b) を適用して、
