各 β2,j には、各々 j = 1、2、...、n に対して 4 つのシンボルがあり、3 つの異なる型の記号がそれぞれにあります。(5) では、各 β3,j には 8 つのシンボルと 4 つの異なる型のシンボルがあります。
(a) と (b) の演算によって βj,i を作成し続ける前に、シンボルの数とさまざまな種類のシンボルの数を決定する規則を学習します。
β2,n と β2,1 には両方とも 4 つのシンボルが含まれているため、β3,1 =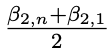 
には 8 つのシンボルが含まれています。β2,n と β2,1 には 3 つの異なるシンボルがありますが、それらは 2 つのシンボルを共有しています。したがって、
β3,1 には 4 つの異なるシンボルがあります。同様に、β2i−1,1 と β2i,1 にはそれぞれ 22i-1 と 22i のシンボルがあります。さらに、続けて有限数列を作成するように、それらには 2i と 2i + 1 の異なるシンボルがあります。
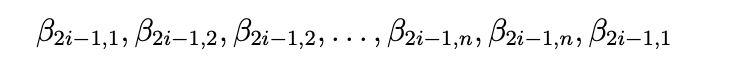
および
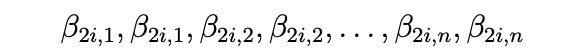
ここで i = 1, 2, . . . および j = 1, 2, . . . , n です。そのため, βn−1,j には n 個の異なるシンボルがあります。故に、(1) により, 各 j = 1, 2, . . . n で,
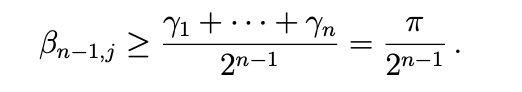
が得られます。次に、演算 (a) と演算 (b) を再度適用します。各角度は 
に収束する事を示していきますが、したがって、 0 に収束する角度の違いを証明しなければなりません。2 つの角度を比較するとき、各々の角度から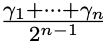 
を減算した後比較できます。
まず、演算 (b) を βn−1,1, βn−1,1,...,βn−1,n、βn−1,n、に適用し、それぞれの角度から 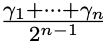を減算します。次に、違い
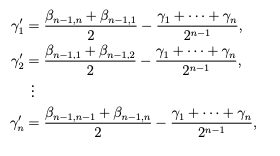
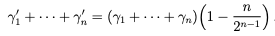
(2)、(3)、(4)、(5)、(6) で使用したのと同様の手順を使用すると、数値 β'i,j が得られ、
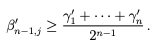
を満たします。
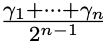を各々の角度から減産し、同様の処理を行うと、
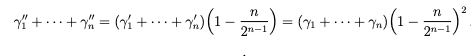
と言った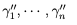 
を得ます。