2.偶数の辺を持つ多角形の面積
n を自然数とする。このセクションでは、辺が 2n の多角形のみを扱います。ここでは、私たちは初等幾何学と数列の限界についての直観的な知識のみを使用します。有限数列には 2 種類の演算が必要です。
定義 1.
任意の有限数列 a1、a2、...、a2n に対する 2 つの演算 (a) と (b) を定義します。
(a) この操作により数列が作成されます。
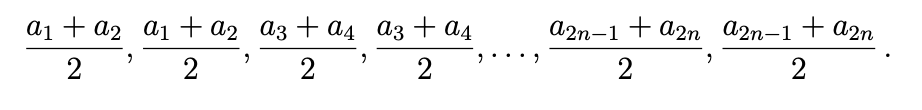
(b) この操作により数列が作成されます。
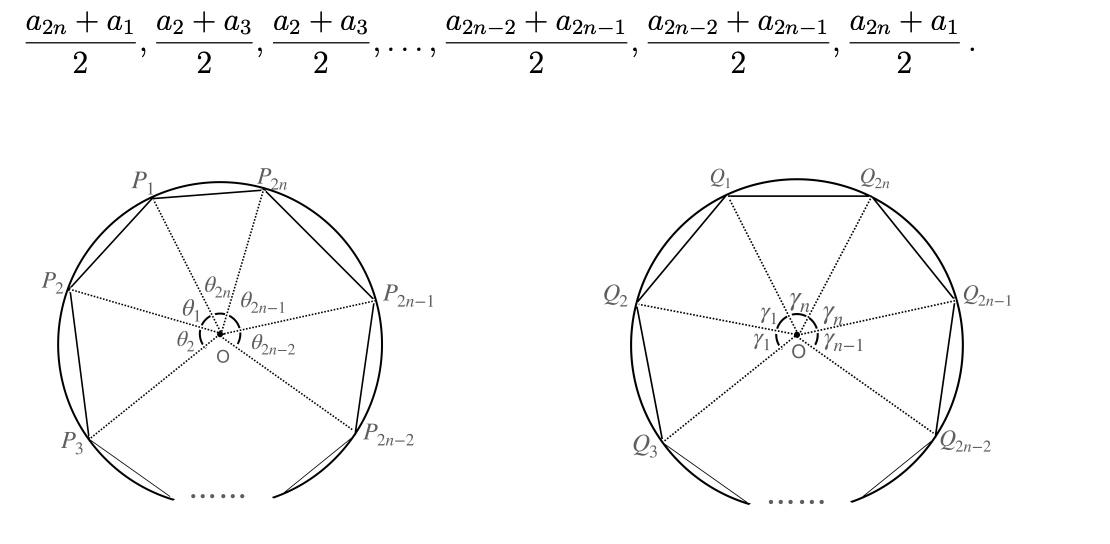
図 2: (a) 操作後の多角形
図 1 と図 2 の円の中心を O とします。まず、図 1 の多角形から始めます。中心角 θ1、θ2、...θ2n に操作 (a) を適用します。それにより、私たちは図 2 の中心角 γ1、γ1、γ2、γ2、... γn の多角形を得ます。この手順は定理 2 の証明に使用されます。
定理 2.
n ≥ 2 の各整数について、指定された円に内接するすべての正 2n 辺多角形の面積が最も大きくなります。
証明。θ1、θ2、...θ2n および γ1、γ2 ... γn は図 1 と図 2 で与えられる角度です。
注意
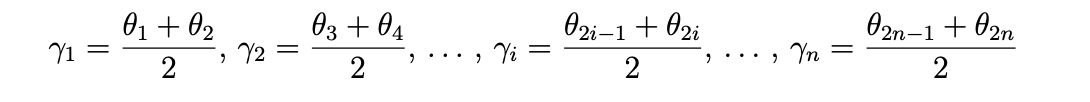
また
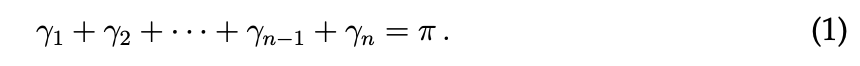
前:1ページ 次:3ページ