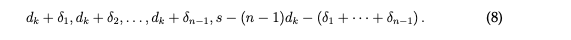
以下の数列に十分の回数 (c)_i の演算を適用した後

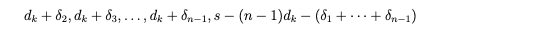
数列 d_k+1 + δ^'₂, d_k+1 + δ^'₃...,d_k+1 + δ^'_n を得、実数の場合 d_k+1, δ^'₂, δ^'₃,...,δ^'_n であり、ここで |δ^'₂|、|δ^'₂|,...,|δ_n| は必要に応じていくらでも小さくすることができます。そして残り (最初) の数は、
s − (n − 1)d_k+1 − (δ^'₂ + δ^'3 + · · · + δ_n） と記載でき、以下の数列を取得します。

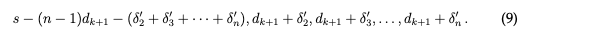
最後の n − 1 個の数値に演算を適用するとき、(8) の最初の要素である d_k + δ₁ の値は変更しませんでした。したがって、 d_k + δ₁ は (9) の最初の要素と等しくなります。

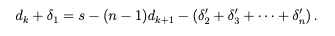
ゆえに

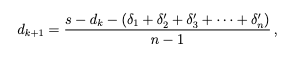
そのため

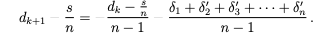
|δ₁ + δ^'₂ + δ^'₃ + ··· + δ^'_n| が十分に小さい場合

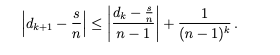
ゆえに各々の m に対し以下が成り立ちます。

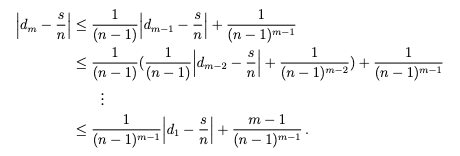
ゆえに m →　∞　の時 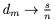となります。証明は帰納法によって続きます。

前：5ページ 次：7ページ