変換
Quartz 2D 描画モデルでは、文書ページを表すユーザ空間と、デバイスのネイティブ解像度を表すデバイス空間の 2 つの完全に独立した座標空間を定義します。ユーザ空間座標は、デバイス空間内のピクセルの解像度とは無関係な浮動小数点数です。文書を印刷または表示する場合、Quartz はユーザ空間座標をデバイス空間座標にマッピングします。したがって、異なるデバイスでの最適な表示のために、アプリケーションの出力を調整するために、アプリケーションを書き直すか、コードを追加する必要は全くありません。
現在の変換マトリックス、つまり CTM を操作することによって、デフォルトのユーザ空間を変更できます。グラフィックスコンテキストを作成すると、CTM は単位配列になります。Quartz 変換関数を使用して CTM を変更し、結果としてユーザ空間の描画を修正できます。
この章では:
- 変換を実行するために使用できる関数の概要を示します。
- CTM を変更する方法を示します。
- アフィン変換を作成する方法について説明します。
- 2 つの変換が同等かどうかを判断する方法を示します。
- ユーザからデバイス空間への変換を取得する方法について説明します。
- アフィン変換の背後にある数学について議論する
Quartz 変換関数について
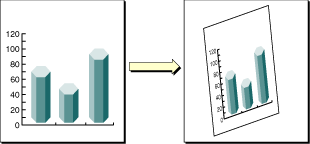
Quartz 2D 組み込み変換関数を使用して、描画を簡単に平行移動、拡大縮小、回転できます。わずか数行のコードで、これらの変換を任意の順序で組み合わせて適用できます。図 5-1 に、イメージの拡大縮小と回転の効果を示します。適用する各変換によって CTM を更新します。CTM は、常にユーザ空間とデバイス空間の間の現在のマッピングを表します。このマッピングによって、あなたのアプリケーションからの出力がどのディスプレイスクリーンやプリンタでも見栄えがよくなります。
図 5-1 拡大縮小と回転の適用
Quartz 2D API には、CTM を取得し変更するための 5 つの関数をが提供しています。CTM を回転、平行移動、および拡大縮小することができ、アフィン変換配列を CTM と連結することができます。現在の変換配列の変更 を参照してください。
Quartz ではまた、変換を CTM に適用するまでは、ユーザ空間上で操作しないアフィン変換を作成することもできます。別の一連の関数を使用してアフィン変換を作成し、これを CTM と連結することができます。アフィン変換の作成 を参照してください。
配列の数学について何も理解せずに、一連の関数を使用することもできます。しかし、変換関数の 1 つを呼び出すときに Quartz が何をするのかを理解したい場合は、配列の背後の数学 を読んでください。
現在の変換配列の変更
CTM を操作して、イメージを描画する前にページを回転、拡大縮小、または平行移動し、描画しようとしているオブジェクトを変形させます。CTM を変換する前に、描画後に復元できるようにグラフィックス状態を保存する必要があります。CTM をアフィン変換と連結することもできます(アフィン変換の作成 を参照)。これらの 4 つの操作(変換、回転、拡大縮小、および連結) は、このセクションで、各操作を実行する CTM 関数とともに説明します。
次のコード行は、有効なグラフィックスコンテキスト、イメージを描画するための長方形へのポインタ、および有効な CGImage オブジェクトを提供すると仮定して、イメージを描画します。このコードは、図 5-2 に示したサンプルの雄鶏のイメージのような画像を描画します。このセクションの残りの部分を読むと、変換を適用するとイメージがどのように変化するかがわかります。
CGContextDrawImage (myContext, rect, myImage);
図 5-2 変換されていないイメージ

平行移動 は座標空間の原点を、x 軸と y 軸で指定した量だけ移動します。CGContextTranslateCTM 関数を呼び出して、各点の x 座標と y 座標を指定された量だけ変更します。図 5-3 は、以下のコード行を使用して、x 軸に 100 ユニット、y 軸に 50 ユニット平行移動したイメージを示しています。
CGContextTranslateCTM (myContext, 100, 50);
図 5-3 平行移動したイメージ

回転 は指定した角度だけ座標空間を移動します。CGContextRotateCTM 関数を呼び出して、回転角度をラジアンで指定します。図 5-4 は、以下のコード行を使用して、ウィンドウの左下にある原点を -45 度回転したイメージを示しています。
CGContextRotateCTM (myContext, radians(–45.));
回転によってイメージの一部がコンテキスト外の位置に移動したため、イメージがクリップされます。回転角度をラジアンで指定する必要があります。
多くの回転を実行する計画がある場合は、ラジアンルーチンを記述すると便利です。
#include <math.h>
static inline double radians (double degrees) {return degrees * M_PI/180;}図 5-4 回転したイメージ

拡大縮小 は、指定した x と y の要素によって座標空間の縮尺を変更し、イメージを効果的に伸縮します。x と y 要素の大きさは、新しい座標が元の座標よりも大きいか小さいかを決定します。さらに、x 要素を負にすることで、座標を x 軸に沿って反転させることができます。同様に、y の要素を負にすることで、y 軸に沿って水平に座標を反転することができます。関数 CGContextScaleCTM を呼び出して、x と y の倍率を指定します。図 5-5 は、x 値が .5 で拡大縮小され、y 値が .75 で拡大縮小されたイメージを示し、コードを以下の行で示しています。
CGContextScaleCTM (myContext, .5, .75);
図 5-5 拡大縮小されたイメージ

連結 は、2 つの配列を、それらを掛け合わせることによって結合します。複数の配列を連結して、配列の累積効果を含む単一の配列を形成することができます。CGContextConcatCTM 関数を呼び出して、CTM とアファイン変換を連結します。アフィン変換と、それらを作成する関数については、アフィン変換の作成 で説明しています。
累積効果を達成する別の方法は、変換呼び出し間でグラフィックス状態を復元せずに、2 つ以上の変換を実行することです。図 5-6 は、以下のコード行を使用してイメージを平行移動してから回転させたイメージを示しています。
CGContextTranslateCTM (myContext, w,h); CGContextRotateCTM (myContext, radians(-180.));
図 5-6 平行移動され回転されたイメージ
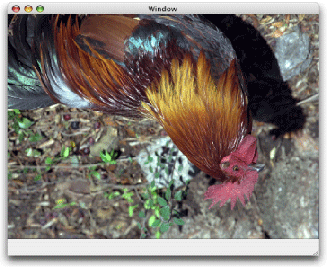
図 5-7 は、以下のコード行を使用して、平行移動、拡大縮小、及び回転されたイメージを示しています。
CGContextTranslateCTM (myContext, w/4, 0); CGContextScaleCTM (myContext, .25, .5); CGContextRotateCTM (myContext, radians ( 22.));
図 5-7 平行移動、拡大縮小、及び回転された画像

複数の変換を実行する順序は重要です。順序を反対にすると異なる結果が得られます。図 5-7 を作成するために使用された変換の順序を逆にすると、このコードで生成された 図 5-8 に示す結果が得られます。
CGContextRotateCTM (myContext, radians ( 22.)); CGContextScaleCTM (myContext, .25, .5); CGContextTranslateCTM (myContext, w/4, 0);
図 5-8 回転、拡大縮小、平行移動されたイメージ

アフィン変換の作成
Quartz で利用可能なアファイン変換関数は、CTM 上ではなく配列上で操作します。これらの関数を使用して、CGContextConcatCTM 関数を呼び出して CTM に後で適用する配列を構築できます。アファイン変換関数は、CGAffineTransform データ構造上で操作するか、またはそれを返します。再利用可能な単純または複雑アフィン変換を構築できます。
アフィン変換関数は、CTM 関数(平行移動、回転、拡大縮小、および連結) と同じ操作を実行します。表 5-1 に、これらの操作を実行する関数をその使用方法の情報と共に示します。平行移動、回転、拡大縮小の各操作には 2 つの関数がある事に注意して下さい。
図 5-1 平行移動、回転、拡大縮小用のアフィン変換関数
| 関数 | 使用 |
|---|---|
| CGAffineTransformMakeTranslation | 原点をどのくらい移動するかを指定する x と y の値から新しい平行移動配列を構築します。 |
| CGAffineTransformTranslate | 既存のアフィン変換に平行移動操作を適用します。 |
| CGAffineTransformMakeRotation | 座標系をどのくらい回転させるかをラジアンで指定する値から新しい回転配列を作成します。 |
| CGAffineTransformRotate | 既存のアフィン変換に回転操作を適用します。 |
| CGAffineTransformMakeScale | 座標を拡大または縮小する量を指定する x および y 値から新しい拡大縮小配列を構築します。 |
| CGAffineTransformScale | 既存のアフィン変換に拡大縮小演算を適用します。 |
Quartz はまた、配列を反転するアファイン変換関数 CGAffineTransformInvert を提供します。反転は一般に、変換されたオブジェクト内の点の逆変換を提供するために使用されます。反転は、配列によって変換された値を復元する必要がある場合に役立ちます。配列を反転し、逆配列で値を掛けると、結果は元の値になります。グラフィックスの状態を保存して復元することによって CTM を変換する効果を元に戻すことができるため、通常は変換を反転する必要はありません。
場合によっては、空間全体を変換するのではなく、点またはサイズだけを変換したい場合があります。関数 CGPointApplyAffineTransform を呼び出すことにより、CGPoint 構造体を操作します。CGSize 構造体を操作するには、CGSizeApplyAffineTransform 関数を呼び出します。CGRect 構造体を操作するには、CGRectApplyAffineTransform 関数を呼び出します。この関数は、渡された長方形の変形された角の点を含む最小の長方形を返します。長方形上で動作するアフィン変換が拡大縮小および平行移動操作のみを実行する場合、返された長方形は 4 つの変換された角から構成された長方形と一致します。
関数 CGAffineTransformMake を呼び出すことで、新しいアフィン変換を作成できますが、新しいアフィン変換を行う他の関数とは異なり、これは配列のエントリの提供を必要とします。この関数を効果的に使用するには、配列の数学を理解する必要があります。配列の背後の数学 を参照してください。
アフィン変換の評価
関数 CGAffineTransformEqualToTransform を呼び出すことで、あるアフィン変換が他のアフィン変換と等しいかどうかを判断できます。この関数は、渡された 2 つの変換が等しい場合は true を返し、そうでない場合は false を返します。
関数 CGAffineTransformIsIdentity は、変換が 恒等変換 であるかどうかを確認するのに便利な関数です。恒等変換では、平行移動、拡大縮小、または回転は実行されません。この変換を入力座標に適用すると、常に入力座標が返されます。Quartz の定数 CGAffineTransformIdentity は、恒等変換を表します。
ユーザをデバイス空間変換に導く
通常、Quartz 2D で描画する場合は、ユーザ空間でのみ作業します。Quartz は、ユーザ空間とデバイス空間の間の変換を行います。Quartz がユーザ空間とデバイスの空間の間で変換するために使用するアフィン変換をアプリケーションが取得する必要がある場合は、CGContextGetUserSpaceToDeviceSpaceTransform 関数を呼び出せます。
Quartz は、ユーザ空間とデバイス空間の間で以下の幾何を変換するためのコンビニエンス関数を多数提供しています。CGContextGetUserSpaceToDeviceSpaceTransform 関数から返されたアフィン変換を適用するよりも、これらの関数は使いやすいかもしれません。
- 点。CGContextConvertPointToDeviceSpace 関数と CGContextConvertPointToUserSpace 関数は、CGPoint データ型をある空間から別の空間に変換します。
- サイズ。CGContextConvertSizeToDeviceSpace 関数と CGContextConvertSizeToUserSpace 関数は、CGSize データ型をある空間から別の空間に変換します。
- 長方形。CGContextConvertRectToDeviceSpace 関数と CGContextConvertRectToUserSpace 関数は、CGRect データ型をある空間から別の空間に変換します。
配列の背後の数学
配列演算の理解が必要な唯一の Quartz 2D 関数は関数 CGAffineTransformMake で、これは 3 × 3 の配列の 6 つの重要なエントリからアフィン変換を行います。あなたが最初からアフィン変換配列を構築することを決して考えていないとしても、変換関数の背後にある数学が興味深いかもしれません。そうでない場合、この章の残りの部分は飛ばせます。
3 × 3 の変換配列-a、b、c、d、tx、及び ty の 6 つの重要な値を、以下の配列で示します。

上記の 3×3 の変換行列が与えられると、Quartz はこの式を使用して点(x、y) を結果の点(x '、y') に変換します。
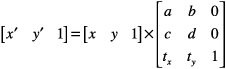
結果は異なる座標系にあり、変換配列の変数値によって変換されます。以下の式は、以前の配列変換の定義です。
![]()
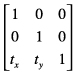
以下の配列は単位配列です。平行移動、拡大縮小、または回転は実行しません。この配列に入力座標を乗算すると、常に入力座標が返されます。

前述の数式を使用すると、この配列が古い点(x、y) と同じ新しい点(x'、y') を生成することがわかります。
![]()
この配列は 平行移動 操作を記述します:
これらは、Quartz が平行移動を適用するために使用する結果の式です。
![]()
この配列は、点(x、y) に対する 拡大縮小 演算を記述します。

これらは、Quartz が座標を拡大縮小するために使用する結果の式です。
![]()
この配列は、点(x、y) を反時計回りに角度 a だけ回転させる 回転 操作を表します。

これらは、Quartz が回転を適用するために使用する結果の式です。
![]()
この式は、回転操作と平行移動操作を 連結 します。
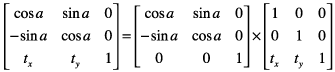
これらは、変換を適用するために Quartz が使用する結果の式です。
![]()
配列を連結する順序は重要であり、配列の乗算は可換ではありません。すなわち、配列 A を配列 B に乗算した結果は、配列 B に配列 A を乗算した結果と必ずしも同じではありません。
前述のように、連結は、アフィン変換行列には 0、0,1 の定数値を持つ第 3 列が含まれているためです。ある配列を別の配列に乗算するには、ある配列の列数は他の配列の行数と一致しなければなりません。これは、2×3 配列と 2× 3配列とは乗算できないことを意味します。したがって、定数値を含む余分な列が必要です。
反転 演算は、変換された座標から元の座標を生成します。与えられた配列 A によって新しい座標(x'、y') に変換された座標(x、y) が与えられた場合、座標(x'、y') を配列 A の逆数で変換すると、元の(x、y) です。配列に逆配列を乗算すると、結果は単位行列になります。
前の章 次の章